Chapter 8: Solving Quadratics and Rootfinding in General

Return to all notes

Absolute and Relative Errors

Consider an algorithm that tries to find the value of $x^{\star}$. If the algorithm actually returns the value $x$, then there will be some error. The absolute error is
$$|x - x^{\star}|$$
and the relative error is
$$\left|\frac{x-x^{\star}}{x^{\star}}\right|.$$

Often, the percent error is helpful as well, which is just the relative error times 100.

Example

Consider an algorithm that returns $x=0.0153$ and the actual answer is $x^{\star}=0.0150$. Find both the absolute and relative errors.

The absolute error is $|0.0153-0.015|= 0.0003$ and the relative error is
$$ \left|\frac{0.0153-0.015}{0.015}\right|=0.02 $$
or 2%.

Rounding Errors and the Quadratic Formula

The following example shows how a well-know formula (the quadratic formula) can lead to incorrect results due to rounding errors.

Remember if you solve $a{x}^{2}+bx+c=0$, the the quadratic formula finds the solution:
$$ x=\frac{-b \pm \sqrt{b^{2}-4ac} } {2a}$$

Next, let’s consider the quadratic equation $12.242{x}^{2}+42.382x+0.0012=0$

We are going to solve this using the quadratic equation in julia

1. Write a function for the quadratic formula.

   qSol = function(a::Number,b::Number,c::Number)
          d=sqrt(b^2-4*a*c)
          return (-b+d)/(2*a),(-b-d)/(2*a)
   end

2. Solve the equation $12.242{x}^{2}+42.382x+0.0012=0$ using 64-bit floating point.

   x1a,x1b = qSol(12.242,42.382,0.0012)

   
   leads to

   (-2.831413841486606e-5,-3.461987696317393)

3. Find the solution if the coefficients are 16-bit floating points.

   x2a,x2b = qSol(Float16(12.242),Float16(42.382),Float16(0.0012))

   
   leads to

   (0.0001448952f0,-3.4615362f0)

4. Assume that the 64-bit answer is correct. Find the absolute and relative errors for the two solutions.

   The absolute errors are

   abs(x1a-x2a) = 0.00017320933367737267
   abs(x1b-x2b) = 0.0004515272652687585

   and the relative errors are:

   abs(x1a-x2a)/abs(x1a) = 6.117414951479887
   abs(x1b-x2b)/abs(x1b) = 0.00013044129635438729

   This shows that the first answer is far off in relative terms.

Exercise

Use the quadratic formula to solve ${x}^{2}-x-110=0$.

Be skeptical of numerical answers

Even though the example above was manufactured to produce bad results, you never know if a numerical solution is accurate or not.

Can we ever be confident of answers?

It’s crucial to have a good sense of the problem (whether it be mathematical or a scientific question). Additionally, testing is an important part of the solution process. We will spend some time later talking about testing.

Let’s change the quadratic formula

I’m going to assume that $b>0$ and let $d=\sqrt{b^{2}-4ac}$. The roundoff occurs when the value of $b$ and $d$ are close to each other. (Note: if $b$ is negative, you can multiply the entire equation through by $-1$ to get $b>0$ without changing the answer.) In the case above, b=42.382 and $d=\sqrt{b^{2}-4ac}=42.38130675663505$. The difference in these is quite small and that is where the round-off error is introduced.

To change the quadratic formula we are going to exchange the addition with a subtraction (however we will not have the catastrophic subtraction error we saw above). “How can you do that you ask?” Here we go…

Start with the quadratic formula (only the + root):
$$ x=\frac{-b + \sqrt{b^{2}-4ac}} {2a}$$

Multiply by a convenient form of 1
$$ x=\frac{-b + \sqrt{b^{2}-4ac}} {2a} \cdot \frac{-b-\sqrt{b^{2}-4ac}}{-b-\sqrt{b^{2}-4ac}}$$

$$ x = \frac{b^{2}-(b^{2}-4ac)}{2a(-b-\sqrt{b^{2}-4ac})}$$

$$ x= \frac{4ac}{2a(-b-\sqrt{b^{2}-4ac})}$$

$$ x = -\frac{2c}{b+\sqrt{b^{2}-4ac}}$$

and there is a similar solution if the - root is taken above. So an alternative quadratic formula is:

qSol2 = function(a::Number,b::Number,c::Number)
  d=sqrt(b^2-4*a*c)
  return -2*c/(b+d),(-2*c)/(b-d)
end

Exercise

• Use the new quadratic formula (qSol2) to find the roots of $x^{2}-x-110=0$. Do you get the same results as above?

• Use the new quadratic formula to solve $12.242{x}^{2}+42.382x+0.0012=0$. Find the absolute and relative errors. Compare your results with that of the standard quadratic formula.

Newton’s Method

Solving an equation is a very important part of mathematics and other scientific fields. However, finding general solutions to equations is not very easy. Consider a cubic equation like $x^{3}-10x^{2}+24x-17$. In the spirit of (but not very simple) the quadratic formula, there is a cubic formula. Much of the wikipedia page spends time solving the cubic with all possibilities. In short, it’s not very easy.

In lieu of using such a formula, a more robust approach is to solve it numerically. Let’s consider

$$15{x}^{3}-143{x}^2+226x+280=0$$

This cubic actually factors, but finding those factors is quite difficult to do in general. We then look at using Newton’s method to solve this. Note the plot below:

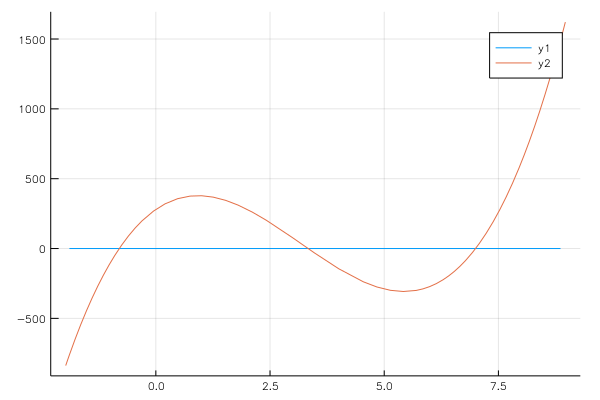
and the three intersection points between the red curve and the blue line (x-axis) are the three roots.

Newton’s method starts with a “guess” at the root and then refines it. Let $x_0$ be the guess, then
$$x_1 = x_0 - \frac{f(x_0)}{f'(x_0)}$$

Let’s look at this in Julia for the function above.

f(x)=15x^3-143x^2+226x+280

and we need the derivative so

df(x)=45x^2-286x+226

Let’s say that x0=0 and find x1 using Newton’s method:

x0 = 0
x1 = x0-f(x0)/df(x0)

returns -1.238938053097345. If we then let x0=x1 and repeat we get a sequence that hopefully gets close to a root (solution). After a few iterations, you should get -0.8

Exercise

• Try to find the other two solutions to this function. (Hint: try different values for x0)

• Write a function using the arguments f,df and x0 and returns the root. The shell of the function should look like

    
  function newton(f::Function,x0::Number)
  
  end
  

and if f and df are functions as defined above, then newton(f,df,0) should return a root of f. Hint: you will need to do the two steps above many times so you will need a loop. Since you don’t know how many times you will need to run through the loop use a while loop and your condition should be that the two steps x0 and x1 are apart from each other. Also checking if two floating point numbers are equal are generally not a good idea, because they have to be equal to all bits.

Using Automatic Differentiation

If you have used Computational Algebra Systems like Maple or Mathematica, you know that computers have the ability to differentiate. Julia is not one of these, although it has some capability of doing some of the feature set of these programs. There is a system called automatic differentiation that will compute the exact derivative to a function at a given point. That is, if you have a function $f(x)$ and a number $a$, it will give you $f'(a)$. The package is called ForwardDiff and you may need to add it and then

using ForwardDiff

For example, if you define:

f(x) =x^2

to find f'(3), type

ForwardDiff.derivative(f,3)

which will return 6. Try something much more complicated:

ForwardDiff.derivative(x->exp(sin(x^2+pi/x)),1.0)

and if you have access to a CAS, see if you answer is correct.

Exercise

1. Adapt your Newton Method code to use Automatic Differentiation. Your function should look like:

   function newton(f::Function,x0::Number)
   
   end

   and you will use the ForwardDiff.derivative inside the while loop.

2. Use your function above to find all three of the roots of the cubic function:
   $$f(x)=15{x}^{3}-143{x}^2+226x+280$$

   Hint: check your answer with the plot shown above.