| Previous Chapter | Return to all notes | Next chapter |
Increasing and Decreasing Functions
Recall that a function is increasing at the point $x$ if $f’(x)>0$ and it is decreasing if $f’(x) \lt 0$. Matlab can help us understand functions and where they are increasing and decreasing using a combination of solving inequalities and taking the derivative.
Here’s an example. Find the intervals where $f(x)=x^{3}-15x^{2}+27x-4$ is increasing the intervals were the function is decreasing. To solve this we will defined the function:
syms x
f(x) = x^3-15*x^2+27*x-4
and then we can find where the function is increasing
S = solve(diff(f(x),x)>0,'ReturnConditions',true)
S.conditions
and the result is \(\left(\begin{array}{c} 9<x\\ x<1 \end{array}\right),\) which can be written in the standard way as $(-\infty,1)\cup(9,\infty)$.
The interval of decrease is found with
S = solve(diff(f(x),x)<0,'ReturnConditions',true)
S.conditions
resulting in \(\left(\begin{array}{c} 1<x\wedge x<9\\ y\in \mathbb{R} \end{array}\right)\) which is the standard interval $(1,9)$.
We can see this using the following plot of the function:
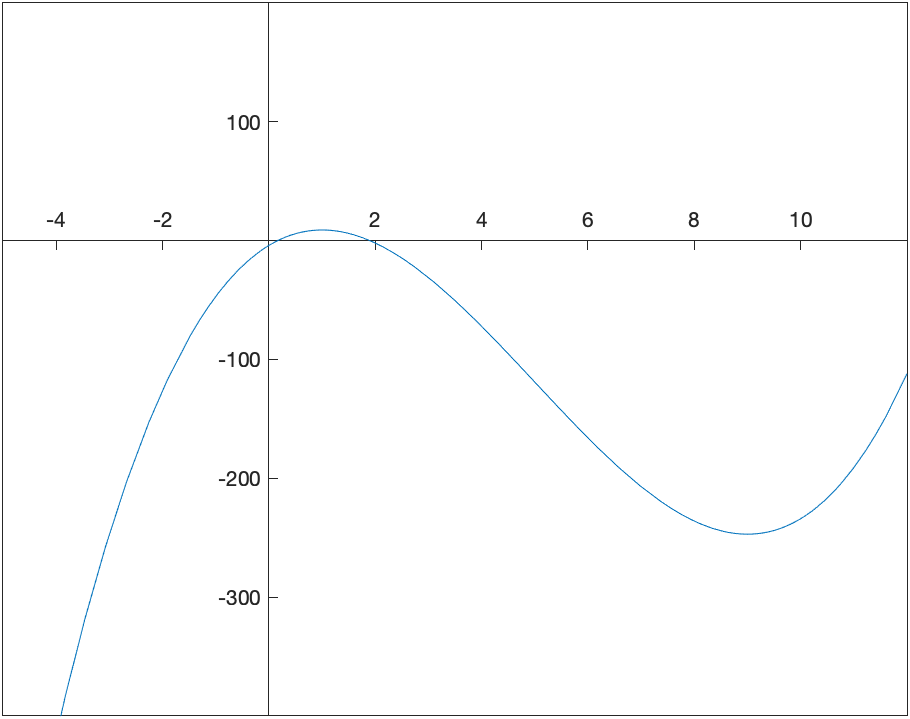
and looking carefully, the function is increasing from $-\infty$ to 1 and then also from 9 to $\infty$. It is decreasing on the interval $(1,9)$.
Mean Value Theorem
Recall that the Mean Value Theorem is as follows:
Let $f$ be a function that is continuous on $[a,b]$ and differentiable on $(a,b)$. There exists a value $c$ in $(a,b)$ such that \(f'( c )=\frac{f(b)-f(a)}{b-a}\)
In short, the MVT says that for nice functions, there is a tangent line that is parallel to the secant line. This is nicely visualized using a CAS like Matlab. Let’s consider the function $f(x)=x^{2}+x$ on the interval $[0,2]$. Since this function is continuous and differentiable everywhere, it satisfies the Mean Value Theorem, and therefore there is a $c$ such that
\(f'( c ) = \frac{f(2)-f(0)}{2-0} = \frac{6-0}{2} = 3\)
and then we can find the $c$ by solving $f’( c )=2c+1=3$ or $c=1$. Next, we plot both the function and the secant line:
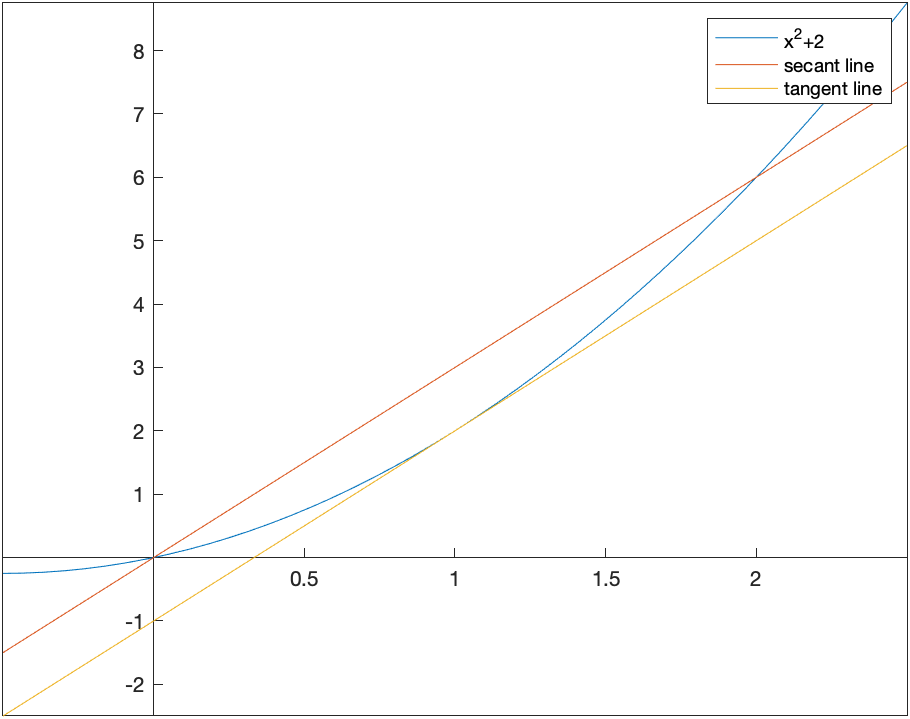
and as can be seen, the tangent line appears to be parallel to the secant line. Whenever the conditions of the Mean Value Theorem are satisified, this has to be true.
Critical value and Relative Extrema
A critical value of a function $f$ is a number $x$ in the domain of the function such that $f’(x)=0$ of $f’(x)$ does not exist.
Find all of the critical points of the function: $f(x)=x^{3}-15x^{2}+27x-4$
In this case, we solve where the derivative is 0.
syms x f
f(x) = x^3-15*x^2+27*x-4
solve(diff(f(x),x)==0)
and Matlab returns $1,9$. Both of the these points are critical points. Since this is a polynomial, the derivative is defined everywhere so there are no places where the derivative is undefined. So the only cricial points are at $1$ and $9$.
Example
| Find all of the critical points of the function $g(x) = | x^{2}-4 | $. |
If we define:
g(x) = abs(x^2-4)
and plot the function:
|  |
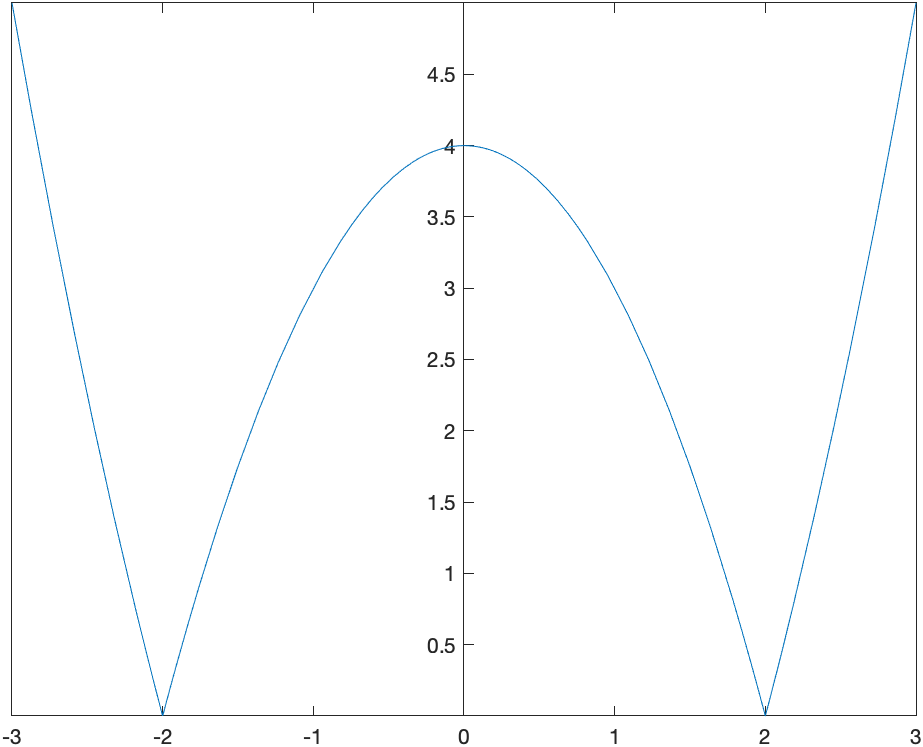Looking at the plot, there is indeed a critical point at $x=0$ because $f’(0)=0$, but it also appears that there are critical points where the derivative is undefined at $x=-2$ and $x=2$.
If we solve where the derivative is 0, then we get:
solve(diff(g(x),x)==0)
so it finds all 3 critical points. I would argue that the derivative of $g$ is not 0, at these points. But they are critical points.
Relative Extrema
A relative minimum of $f$ is a number $f( c )$, such that $f(x) ≥ f( c )$ for all $x$ near $c$. A relative maximum of $f$ is a number $f( c )$, such that $f(x) \leq f( c )$ for all $x$ near $c$. The term relative extrema is either a relative minimum or maximum.
As an example, let’s return to the function $f(x)=x^{3}-15x^{2}+27x-4$. From the plot reproduced here:
There appears to be a relative minimum of $f(9)=-239$ and a relative maximum of $f(1)=17$. As always it’s very difficulty to tell exactly the location(s) of relative extrema.
Theorem: First Derivative Test A number $f( c )$ is an relative minimum if $c$ is a critical value and $f’(x) \lt 0$ for $x \lt c$ and $f’(x) \gt 0$ for $x \gt c$. A number $f( c )$ is a relative maximum if $c$ is a critical value and $f’(x) \gt 0$ for $x \lt c$ and $f’(x) \lt 0$ for $x \gt c$.
In short, if $c$ is a critical value and if $f’$ switches sign from positive to negative, then $f( c )$ is a relative maximum. If $f’$ switches sign from negative to positive, then $f( c )$ is a relative minimum.
Often, we can build a chart of the value of the derivative and let’s let Matlab help us do this.
First, recall that we found the critical values of the function to be $1,9$. If we pick a value to the left of 1, between 1 and 9 and to the right of 9 and evaluate the derivative, we can determine that in fact, we have relative minima and maxima. We included 0, 5 and 12 and then made sure they are in increasing order like:
xvals=[0 1 5 9 12]
then the following will evaluate the derivative at these points:
syms x f
f(x) = x^3-15*x^2+27*x-4
df(x) = diff(f(x),x)
fprime = arrayfun(@(x) df(x),xvals)
[xvals; fprime]'
which returns the matrix: \(\begin{array}{cc} 0&27\\ 1&0\\ 5&-48\\ 9&0\\ 12&99\end{array}\) where the first column is the $x$ values that we chose and the second column is $f’(x)$. The derivative goes from positive to negative across $x=1$, so that is a location of a relative maximum. And the derivative goes from negative to positive across $x=9$, so that is a relative minimum.
Example: Finding relative extrema
Find all relative extrema of $g(x)=\left\vert x^{2}-4\right\vert$.
From above, the critical point are $-2,0,2$. And if we repeat the steps above:
xVals=[-3,-2,-1,0,1,2,3]
where we have chosen points greater than and less than each of the critical points.
g(x) = abs(x^2-4);
dg(x) = diff(g(x),x);
gprime = arrayfun(@(x) dg(x),xvals);
[xvals; gprime]'
where the last expression makes the table print out nicer. The result returns
\[\begin{array}{cc} -3 & -6 \\ -2 & 0 \\ -1 & 2 \\ 0 & 0 \\ 1 & -2 \\ 2 & 0 \\ 3 & 6 \end{array}\]where the first column are the $x$ values and the second column is $g’(x)$. This shows that the derivative is 0 when $x=2$ and $x=-2$ (which is not true), but anyway… The derivative switches sign from negative to positive at $x=-2$, so it is relative min, the derivative switches sign from positive to negative at $x=0$, so it is a relative max and the derivative switches sign from negative to positive at $x=2$, so it is a relative min.
Exercise
Find all relative extrema of $\sqrt[3]{x^{3}-4x}$. Hint: use the nthroot function to get Matlab to handle the cube root correct. First, find the extrema using the definition and determine if each is either a relative minimum, maximum or neither. You can verify the results with a plot at the end.
Concavity of a Graph and Inflection points
A graph of a function $f$ is concave up at the point $x$ if it’s derivative is increasing or $f^{\prime\prime}(x)>0$. A graph of a function $f$ is concave down at the point $x$ if it’s derivative is decreasing or $f^{\prime\prime}(x)\lt 0$.
Example
Find the intervals on which the function $f(x)=x^{4}-6x^{2}-1$ is concave up and concave down.
First, recall that to find a second derivative if
f(x) = x^4-6*x^2-1
then $f^{\prime\prime}$ can be found with
d2f(x) = diff(f(x),x,2)
To solve where the graph is concave up, we
S = solve(d2f(x)>0,'ReturnConditions',true)
S.conditions
which is interpreted as $(-\infty, -1) \cup (1,\infty)$. The graph is concave down can be found with
S = solve(d2f(x)<0,'ReturnConditions',true)
S.conditions
can be interpreted as $(-1,1)$.
Recall that an inflection point of a function is a $x$-coordinate where a graph flips from concave up to concave down or vise versa. You look for the values where $f^{\prime\prime}(x)=0$ or $f^{\prime\prime}(x)$ is undefined.
Since the second derivative is continuous (it is a polynomial), the only places where there might be inflection points is where $f^{\prime\prime}(x)=0$. These can be found with Matlab with
solve(d2f(x)==0)
and this returns $-1,1$. As you can see above, it switches concavity at both of these points.
Let’s take a look at the graph:
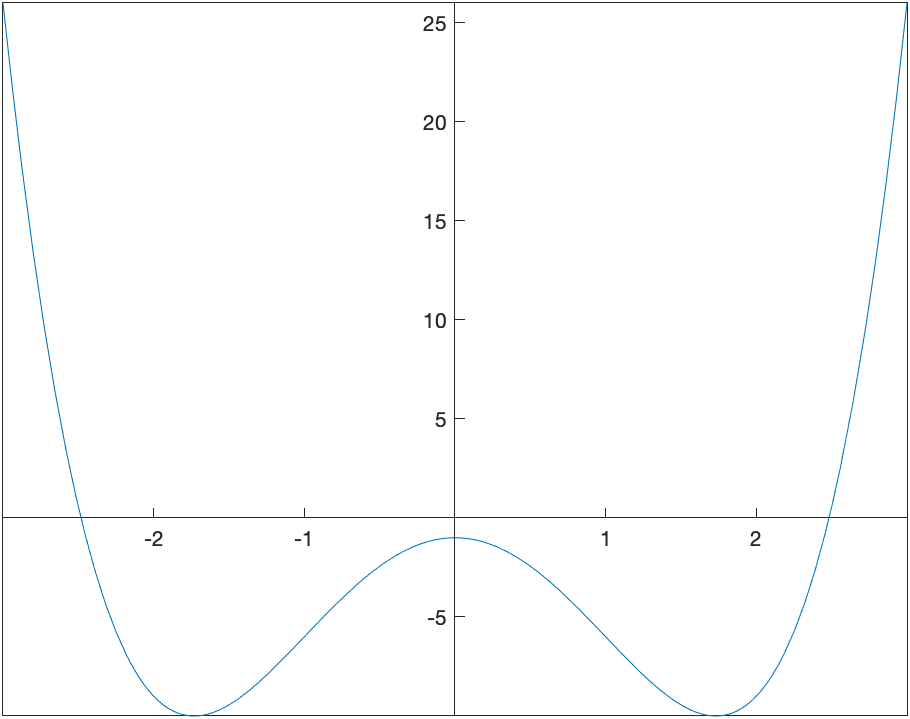
and should be able to see that the graph switches concavity at both $x=-1$ and $x=1$.
Relative Extrema and the Second Derivative
There is an alternative way to test for relative extrema by using the second derviative. Generally, it’s often easier to use if the second derivative exists.
Theorem: Second Derivative Test If $f’( c )=0$ and $f^{\prime\prime}(c )>0$, then $f( c )$ is a relative minimum. If $f’( c )=0$ and $f^{\prime\prime} ( c ) < 0$, then $f( c )$ is a relative maximum.
Example: Finding relative extrema and 2nd derivatives
Use the theorem above to find the relative extrema of $f(x)=x^{3}-15x^{2}+27x-4$. Let’s define it and its first and second derivatives:
f(x)=x^3-15*x^2+27*x-4
df(x) = diff(f(x),x)
d2f(x) = diff(f(x),x,2)
Again, if we find the $x$ values where the derivative is 0 (Note: we did this above), using:
solve(df(x)==0,x)
we get $1,9$ again. And
d2f(1)
d2f(9)
returns $-24,24$, which shows $f^{\prime\prime}(1)= -24$, $f(1)$ is a relative maximum and since $f^{\prime\prime}(9)=24$, then $f(9)$ is a relative minimum.
Example: Relative extrema of a non-differentiable function
Can we use the above theorem to find the relative extrema of $g(x)=\vert x^{2}-4\vert$?
We can for the critical value of $x=0$ and since $g^{\prime\prime}(0)=-2$, then $g(0)$ is a relative maxmium. However, since the derivative (and therefore second derviative) is not defined at $x=-2$ and $x=2$, then we can’t use this theorem for these critical points. The First Derivative Test still holds though for this example.
Exercise
Let $f(x)=e^{-x}(x^{2}-6x-6)$. Find all critical values of $f$ and use the second derivative test to classify each as a local min or max.
Absolute Maxima and Minima
Extreme Value Theorem
If $f$ is continuous on a closed interval $[a,b]$, then $f$ attains an absolute maximum value $f( c )$ and an absolute minimum $f(d)$ at some numbers $c$ and $d$ in $[a,b]$.
Closed Interval Method
The following steps will find the absolute maximum and minimum:
-
Find all critical values of $f$.
-
Evaluate $f$ on all points in 1) within the interval as well as the two endpoints.
-
The smallest function value in 2) is the absolute min and the largest is the absolute maximum.
Example: Absolute Max and Mins
Find the absolute maximum and minimum of $g(x)=\vert x^{2}-4\vert$ on the interval $[-1,4]$
-
The critical values of $g$ are $-2,0$ and $2$ (see above)
-
We evaluate $g$ at only the values $0$ and $2$ from 1) because $-2$ is not in the interval $[-1,4]$ and the values $-1$ and $4$, the endpoints from the interval.
To do this in Matlab
g(x) = abs(x^2-4)
dg(x) = diff(g(x),x)
xVals=[0,2,-1,4]
gvals = arrayfun(@(x) g(x),xVals)
[xVals; gvals]'
returns
\[\left[\begin{array}{cc} 0 & 4 \\ 2 & 0 \\ -1 & 3 \\ 4 & 12 \end{array}\right]\]The smallest function value is 0, so this is the absolute minimumum and the largest function value is 12, so this is the absolute maximum. The absolute minimum occurs at $x=2$ and the absolute maximum occurs at $x=4$.
Example: Maximize Application
Find the dimensions of the rectangle with the largest area that fits underneath the function $f(x)=\sqrt{4-x^{2}}$ and the base of the rectangle is on the $x$-axis. The following plot shows a possible rectangle and the function (top half of a circle):
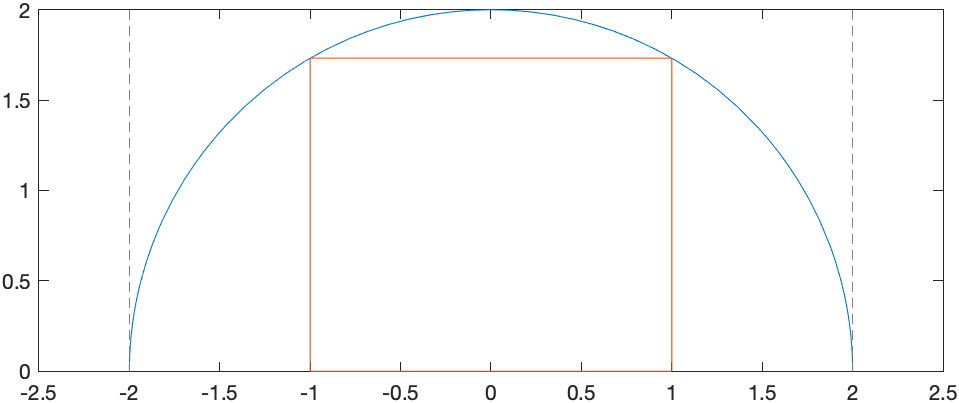
Let half of the width of the rectangle be $x$ (so the height is $f(x)$). Therefore the area is \(A=2xf(x)=2x\sqrt{4-x^{2}}\) and we seek to find the absolute maximum of this function.
Note that since no interval was given, we will use the domain of the function as the domain. Since the square root must be greater than or equal to 0, the domain is
S = solve(4-x^2>=0,'ReturnConditions',true);
S.conditions
results in the interval $[-2,2]$, so this is the interval for the closed interval method.
The first step is to find the critical points. Let
A(x) = 2*x*sqrt(4-x^2)
and find where the derivative is zero.
dA(x) = diff(A(x),x)
solve(dA(x)==0)
results in $[-\sqrt{2},\sqrt{2}]$.
The second step is to evaluate the function at all the critical points as well as the endpoints (which are $-2$ and $2$, the same as two of the critical points.)
xValues = [sym(-sqrt(2)) sym(sqrt(2)) sym(-2) sym(2)];
areaValues = arrayfun(@(x) A(x),xValues);
[xValues; areaValues]'
results in \(\left[\begin{array}{cc} -\sqrt{2} & -4 \\ \sqrt{2} & 4 \\ -2 & 0 \\ 2 & 0 \end{array}\right]\)
so the absolute maximum is $4$ and occurs when $x=\sqrt{2}$.
Recall that the question asked for the dimensions of the rectangle. So the width is $2x$ which is $\sqrt{2}$ and the height is $f(\sqrt{2})= \sqrt{2}$.
Exercise: Maximum Application
A can is in the shape of a right circular cylinder. What are the dimensions (radius and height) of the can that holds 1000 $\text{cm}^{3}$ of liquid and uses the smallest amount of material. Note: in this case, you don’t need a closed interval, but you should show that the amount of material (or the surface area) is a minimum by using the second derivative test.
Using the built-in maximum and minimum function
Matlab also has the ability to find the minimum of a function for a given interval. For example to repeat finding the absolute minimum and maximum values of $g(x)=\vert x^{2}-4\vert$ on the interval $[-1,4]$, we can type
[xmin fmin] = fminbnd(@(x) abs(x^2-4),-1,4)
which returns 2 for xmin and about 0 for fmin, the function value. We can find the max by finding the minimum of the negative number or:
[xmax fmax] = fminbnd(@(x) -1*abs(x^2-4),-1,4)
which returns about 0 for xmax and -4 for fmax, which means the function value would be 4. However this didn’t find the maximum on the interval. It just found a local max.
Using Calculus to find accurate plots
This section also shows that we can use Calculus to help us find a good plotting window. Consider the following function: \(f(x)=3x^{4}+320x^{3}+3000x^{2}-600000x+5000\)
If we just plot it in Matlab, we get:
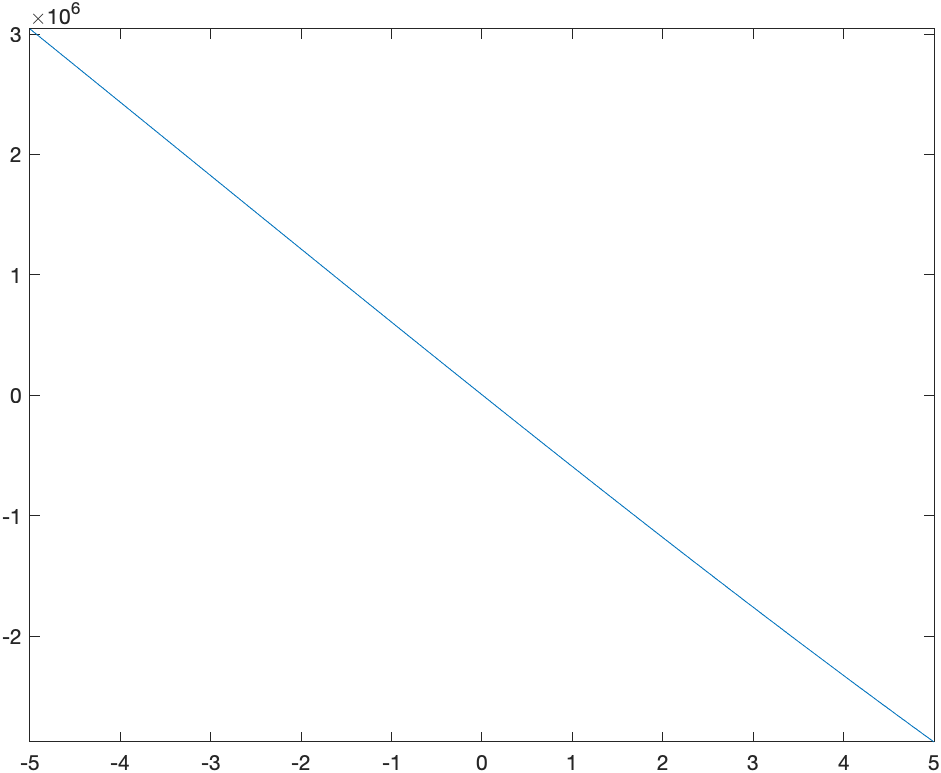
which doesn’t look right. It’s a quartic (because of the largest power of $x$) with positive $x^{4}$ term so it should be a bit like $x^{2}$ for large $\vert x\vert$.
We could blindly poke around for a good plotting window, but instead we’ll find any important features. First, let’s find the critical points.
syms x
f(x) = 3*x^4+320*x^3+3000*x^2-600000+5000
df(x) = diff(f(x),x)
solve(df(x)=0)
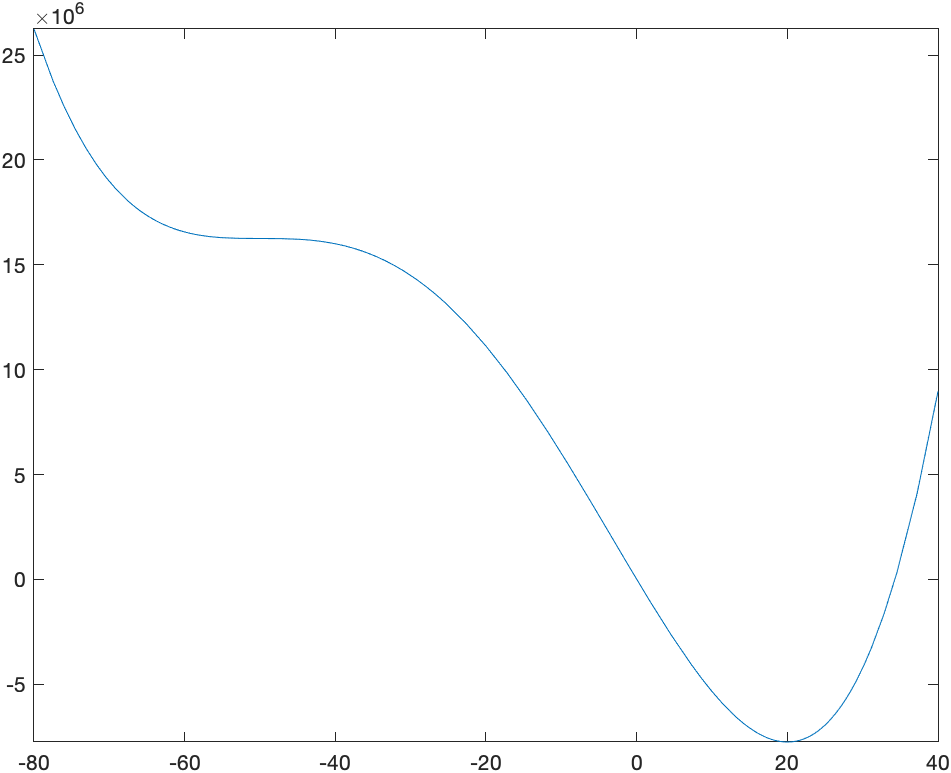
results in $20,-50,-50$, so there are two critical points. If we make sure we include these,
plot(f(x), [-80 40])
we get the following plot:
Another Example
Plot $g(x)=10000x^{5}-x^{3}$.
Again, a plot of this results in
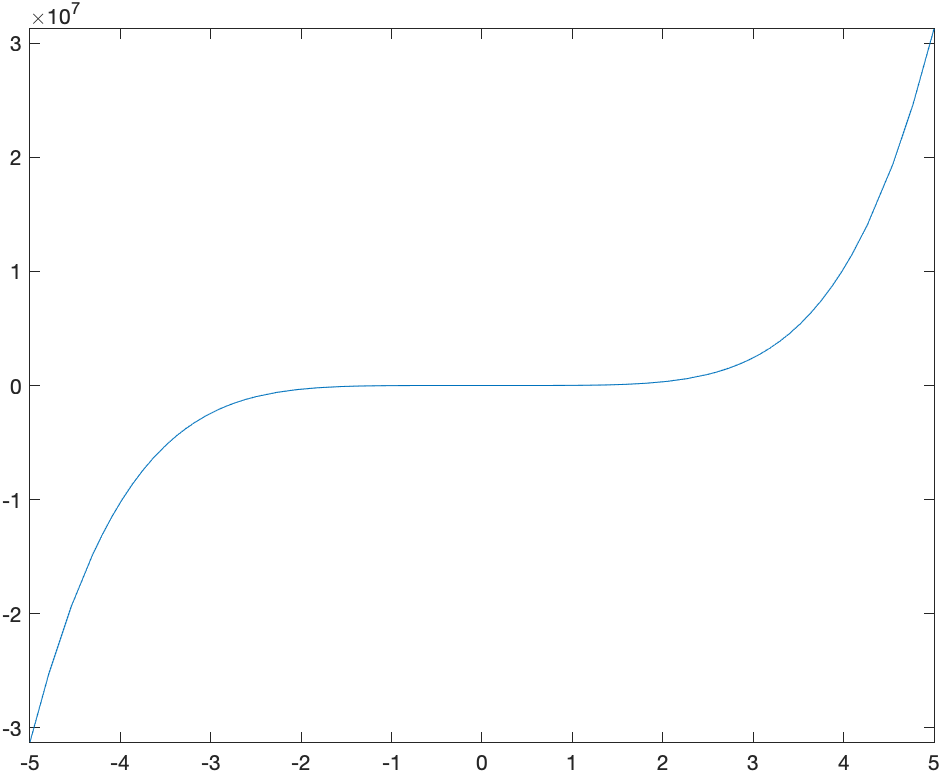
How do we know if this is correct? A little knowledge of a function with $x^{5}$ as the leading term means that it could be right because it may look like $x^{3}$, but it’s hard to tell. Let’s check for critical points.
dg(x) = diff(g(x),x)
crit_pts = solve(dg(x)==0)
results in \(0, 0, \frac{\sqrt{15}}{500}, -\frac{\sqrt{15}}{500}\) and then making this a decimal approximation
double(crit_pts)
and the result is \(\left[\begin{array}{rrrr}0 & 0 & 0.0077 & -0.0077\end{array}\right]\) so the critical points are not visible on the previous plot. In this case, if we change the plotting window using
fplot(g(x), [-0.011 0.011])
we get the plot
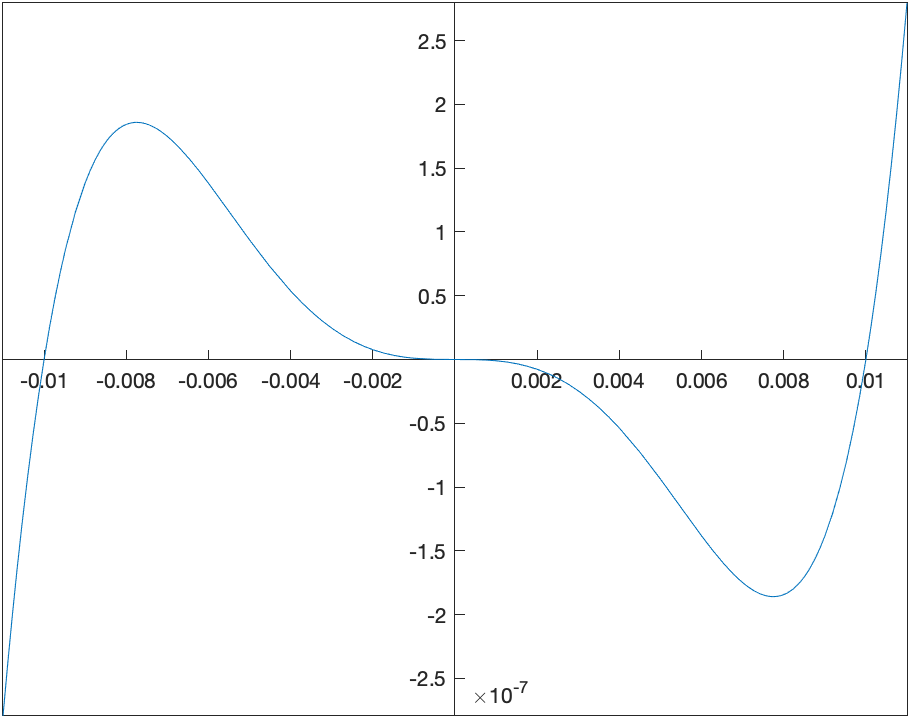
One more example
Lastly, let’s look at the plot of \(h(x)=\frac{1}{x^{8}}-200000000\frac{1}{x^{4}}\) where the standard plot looks like:
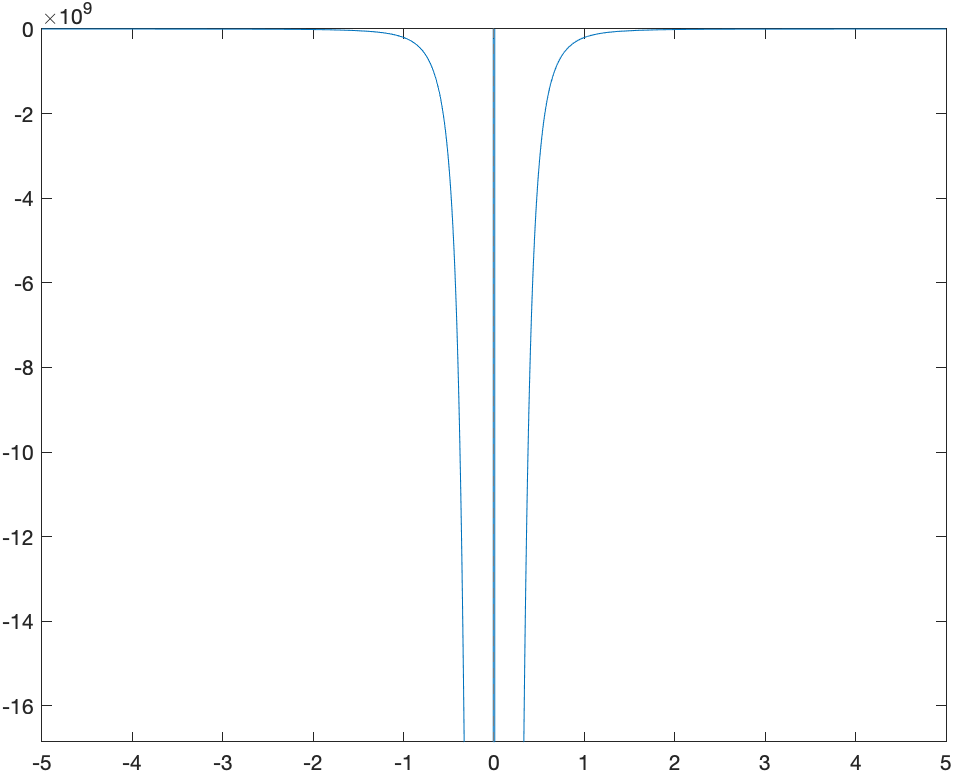
Again, is this the right plot?
Let’s start looking for the $x$-intercepts.
[num,den] = numden(h(x))
vpasolve(num==0)
where we have used vpasolve because an approximate location is sufficient and the function is 0 where the numerator is 0. The result is
\(\left(\begin{array}{c}
-0.0084089641525371454303112547623321\\
0.0084089641525371454303112547623321\\
-0.0084089641525371454303112547623321\,\mathrm{i}\\
0.0084089641525371454303112547623321\,\mathrm{i}
\end{array}\right)\)
and there were two others that are imaginary.
The critical points:
dh(x) = diff(h(x),x)
vpasolve(dh(x)==0)
results in \(\left(\begin{array}{c} -0.01\\ 0.01\\ -0.01\,\mathrm{i}\\ 0.01\,\mathrm{i} \end{array}\right)\) where the last two are imaginary.
If we plot to include these points,
fplot(h(x),[-0.012 0.012])
we get:
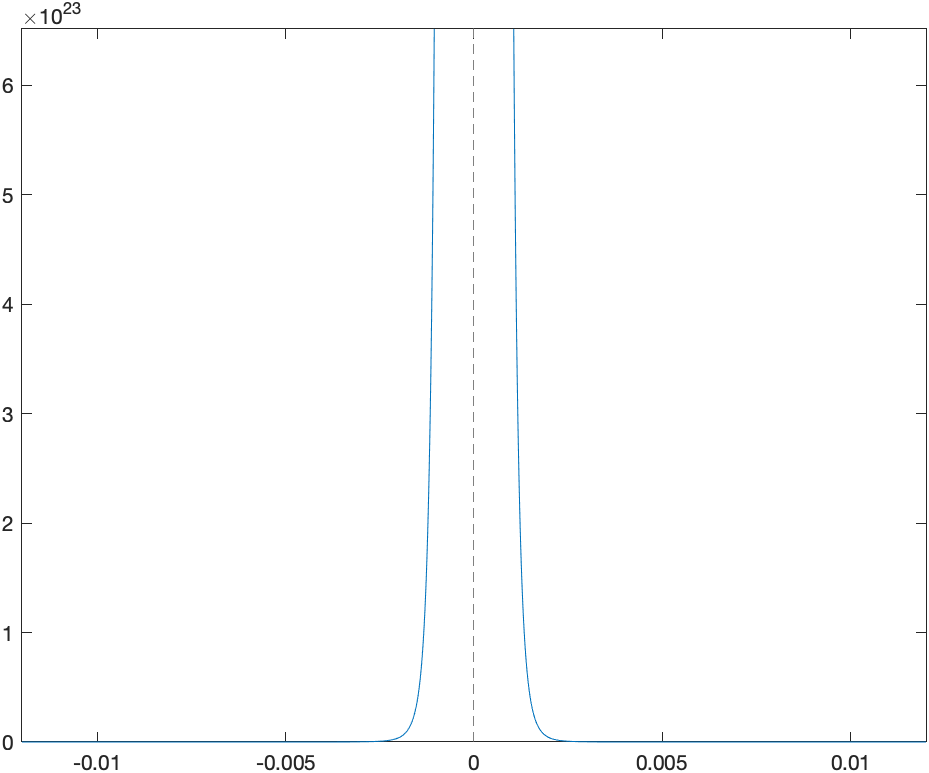also I don’t see any of the critical points. Notice the y range on this is HUGE.
Next, let’s change the vertical range. We want to make sure that we are including the $y$-values of the critical points.
h(0.01)
h(-0.01)
both return $-1.000 10^{16}$. If we then do
fplot(h(x),[-0.012 0.012])
ylim([-2e16 2e16])
set(gca, 'XAxisLocation', 'origin', 'YAxisLocation', 'origin')
we get
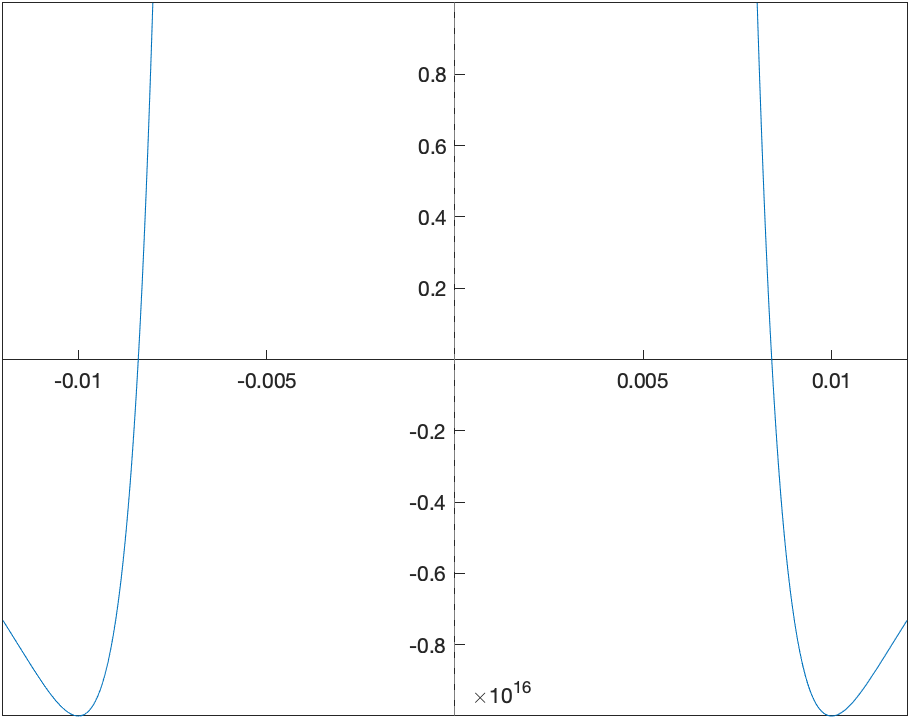
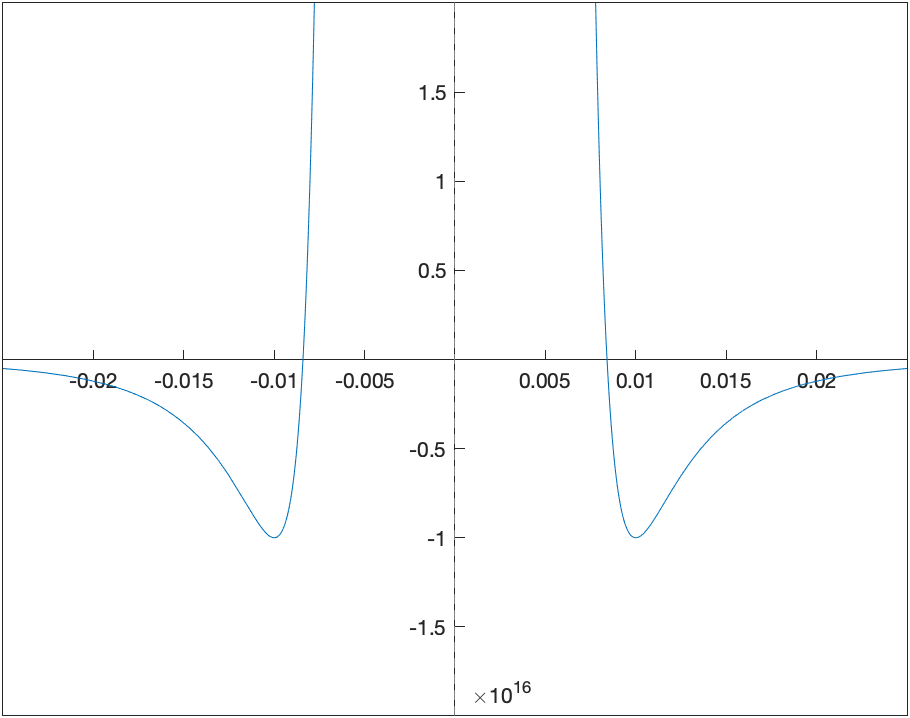
which is better, but tinkering a bit more
fplot(h(x),[-0.025 0.025])
ylim([-2e16 2e16])
set(gca, 'XAxisLocation', 'origin', 'YAxisLocation', 'origin')
results in
| Previous Chapter | Return to all notes | Next chapter |